A descriptive text for the image
TL;DR: We amplify the tangential part of each sampler update while keeping the radial term unchanged, steering trajectories along higher-density regions, resulting in higher-quality samples.

Overview

Diffusion models often hallucinate by drifting off the data manifold. Tangential Amplifying Guidance (TAG) is a plug-and-play, architecture-agnostic inference method that amplifies the tangential component of each update while preserving the radial term, steering trajectories toward higher-density regions and improving fidelity without extra model evaluations.

Conceptual Visualization of TAG

A descriptive text for the image

While standard sampling produces hallucinations by drifting into low-probability areas, TAG guides the generation process toward high-probability regions, resulting in higher-quality samples.

Motivation

A descriptive text for the image

Our motivation stems from Tweedie's formula, which reveals that the score function, \(\Delta_x \log p(x\mid t_k)\), points toward high-probability data regions. Our goal is to emphasize this 'data term' without perturbing the scheduler's prescribed noise schedule.

What is implied by “Tangential”
(i.e., Data Term)?

We visualize each latent per timesteps. The original update \(\Delta_k:=\boldsymbol{x}_{k-1}-\boldsymbol{x}_{k}\) contains a mix of structural information and noise. We decompose this update into a normal component \(P_{k}\Delta_k\) and a tangential component \(P^{\perp}_{k}\Delta_k\). Normal component is largely unstructured and noisy, while Tangential component clearly preserves the primary semantic structure.

A descriptive text for the image

Visualization of Normal \(P_{k}\Delta_k\) and Tangential \(P^{\perp}_{k}\Delta_k\) Components. Tangential components contains rich semantic informations.

Toy Experiment

Without proper guidance, sampling trajectories drift off the data manifold, creating fragmented or OOD results. While common fixes like CFG can help, they often oversimplify the geometry or leave stray artifacts. In contrast, TAG effectively steers the sampling process along high-density branches of the data, suppressing outliers, thus achieving the result most faithful to the ground truth.

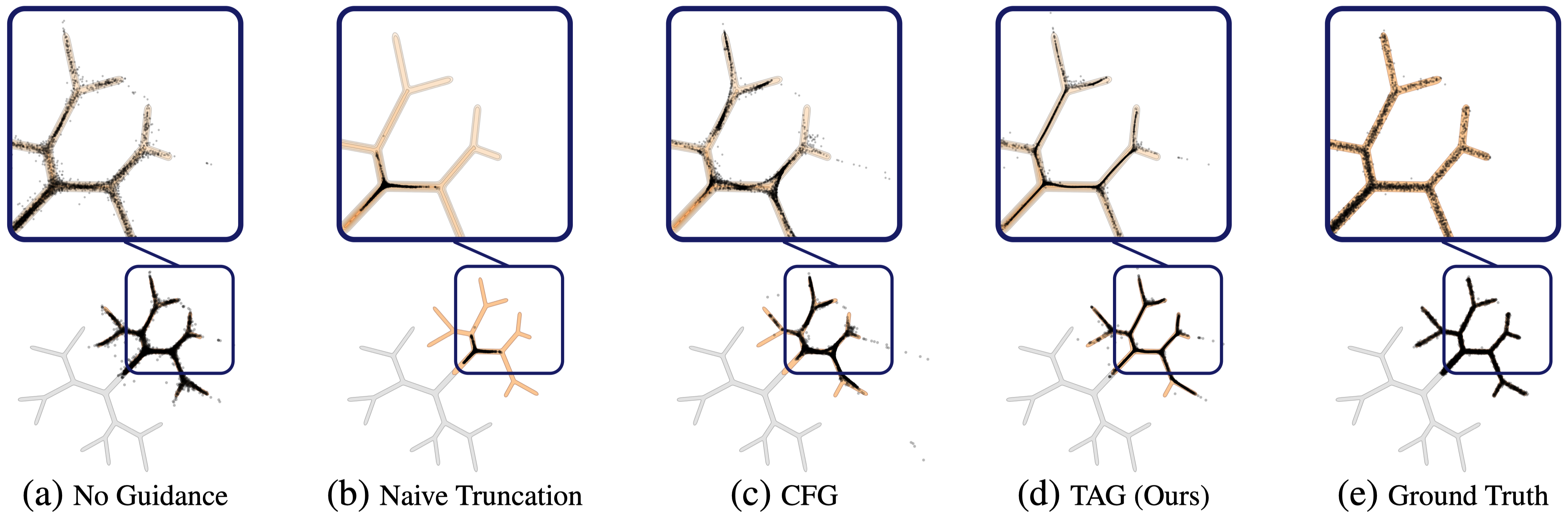
Comparisons diagram

Sampling on a 2D branching distribution (Karras et al., 2024) under different guidance methods. TAG effectively steers sampling trajectories toward high-density regions along the branches, suppressing off-manifold outliers to achieve the highest similarity to the ground truth distribution.

Theorem

Overall framework

We prove that amplifying the tangential component monotonically increases the first-order Taylor gain of the log-likelihood, which effectively steers the sampling trajectory toward higher-density regions of the data manifold. Specifically:

(i) The first-order Taylor gain is a monotonically increasing function of the tangential amplification factor (η).The theorem shows that the derivative of the gain with respect to η is always non-negative. This mathematically confirms that increasing the tangential amplification consistently increases (or maintains) the movement toward high-probability regions.
(ii) The gain increment from a TAG step is always greater than or equal to that of a standard base step. The analysis explicitly shows that the difference in gain between a TAG-modified step and the base step is non-negative, with equality only holding if no amplification is applied (η=1). This guarantees that TAG provides a direct improvement in log-likelihood gain at each step of the sampling process.

Experimental results

We apply TAG at inference on pretrained backbones: Stable Diffusion v1.5 for the main experiments and Stable Diffusion 3 for flow matching. Unconditional results are reported on ImageNet-1K val; text-conditional results use MS-COCO 2014 val.

Unconditional Generation with SD 1.5

Table 1. Quantitative results across previous guidance methods and +TAG sampling settings for unconditional generation
(ImageNet val, 30K samples, SD v1.5, DDIM).
Methods Guidance Scale TAG Amp. (η) #NFEs #Steps FID ↓ IS ↑
DDIM (Song et al., 2020a) – – 50 50 76.942 14.792
DDIM + TAG – 1.05 50 50 67.971 16.620
DDIM + TAG – 1.15 50 50 67.805 16.487
DDIM + TAG – 1.25 50 50 71.801 15.815
SAG (Hong et al., 2023) 0.2 – 50 25 71.984 15.803
SAG + TAG 0.2 1.15 50 25 65.340 17.014
PAG (Ahn et al., 2024) 3 – 50 25 64.595 19.30
PAG + TAG 3 1.15 50 25 63.619 19.90
SEG (Hong, 2024) 3 – 50 25 65.099 17.266
SEG + TAG 3 1.15 50 25 60.064 18.606

Unconditional Generation with SD 2.1 & SDXL

Table 2. Quantitative results of TAG on various Stable Diffusion baselines (10K ImageNet val, DDIM 50 NFEs).
Methods TAG Amp. (η) #NFEs #Steps FID ↓ IS ↑
SD v2.1 (Rombach et al., 2022) – 50 50 100.977 11.553
SD v2.1 + TAG 1.15 50 50 88.788 13.311
SDXL (Podell et al., 2024) – 50 50 124.407 9.034
SDXL + TAG 1.20 50 50 113.798 9.716

Unconditional Generation with Flow Matching (SD3)

Table 3. Quantitative results for flow matching–based generator (ImageNet val, 30K samples; all images generated with 50 NFEs).
Methods w/ SD3 TAG Amp. (η) FID ↓ IS ↑
Esser et al. (2024) – 96.383 11.831
+ TAG 1.05 91.706 12.274

Unconditional Generation with fewer NFEs

Table 4. Quantitative results for unconditional image generation on ImageNet (SD v1.5). Metrics on 30K samples;
inference time averaged over 100 runs (RTX 4090).
Methods TAG Amp. (η) #NFEs Inference Time (s) FID ↓ IS ↑
DDIM (Song et al., 2020a) – 50 1.9507 76.942 14.792
DDIM + TAG 1.15 25 1.0191 72.535 15.528
DDIM + TAG 1.15 50 1.9674 67.805 16.487
DPM++ (Lu et al., 2025) – 10 0.4433 85.983 13.037
DPM++ + TAG 1.15 10 0.4522 74.238 14.930

Conditional Generation with MS-COCO2014

Table 5. Quantitative results across guidance-only (CFG, PAG, SEG) and guidance w/ TAG on MS-COCO 2014 val (10k random text prompts). All images sampled with Stable Diffusion v1.5 using the DDIM sampler; cfg_scale=2.5, pag_scale=2.5, seg_scale=2.5.
Methods TAG Amp. (η) #NFEs #Steps FID ↓ CLIPScore ↑
Condition-Only – 30 30 85.145 19.77 ± 3.43
Condition-Only + TAG 1.2 30 30 58.438 21.88 ± 2.99
CFG (Ho & Salimans, 2021) – 100 50 26.266 22.60 ± 3.28
CFG + C-TAG 2.5 30 15 23.414 22.82 ± 3.21
PAG (Ahn et al., 2024) – 50 25 24.280 22.72 ± 3.25
PAG + C-TAG 1.25 50 25 22.109 22.07 ± 3.49
SEG (Hong, 2024) – 50 25 29.215 18.17 ± 3.55
SEG + C-TAG 1.25 50 25 23.446 16.94 ± 3.96

Visualization of TAG on various Diffusion Backbone

Qualitative results on Stable Diffusion 1.5
Qualitative results on Stable Diffusion 2.1
Qualitative results on Stable Diffusion XL
Qualitative results on Stable Diffusion 3

Conclusion

This paper introduces a new perspective for addressing the problem of hallucinations in diffusion models, demonstrating that the tangential component of the sampling update encodes critical semantic structure. Based on this geometric insight, we propose Tangential Amplifying Guidance (TAG), a practical, architecture-agnostic method that amplifies the tangential component. By doing so, TAG effectively steers the sampling trajectory toward higher-density regions of the data manifold, generating samples with fewer hallucinations and improved fidelity. Our method achieved good samples without requiring retraining or incurring any additional heavy computational overhead, offering a practical, plug-and-play solution for enhancing existing diffusion model backbones.

Citation

If you use this work or find it helpful, please consider citing: 

@misc{cho2025tagtangentialamplifyingguidancehallucinationresistant,
      title={TAG:Tangential Amplifying Guidance for Hallucination-Resistant Diffusion Sampling}, 
      author={Hyunmin Cho and Donghoon Ahn and Susung Hong and Jee Eun Kim and Seungryong Kim and Kyong Hwan Jin},
      year={2025},
      eprint={2510.04533},
      archivePrefix={arXiv},
      primaryClass={cs.CV},
      url={https://arxiv.org/abs/2510.04533}, 
}